Looking at the pictures on the website of Spacecollective I was fascinated by the pictures of patterns and structures. Most of these pictures where pictures with a high degree of symmetry. This started my research to look into the topic of symmetry.
Structures with symmetry most of the times seem to have something that is called visual esthetics. These structures have been a topic of study for centuries. It appeared that most structures consisted out of geometrical shapes that can be split into parts each of which is a reduced-sized copy of the whole. So the structure is build out of an infinite number of copies of the geometrical shape. Structures that have this quality are called fractals. The fractal is the perfect self symmetry. This perfect similarity can be described with a mathematical equation that undergoes iteration. So it seems that there is a language that can describe the perfect similarity to some extent.
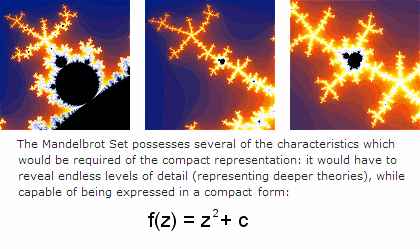
To look more in to this language of similarity I researched one of the most fascinating fractals, the Mandelbrot fractal. Everywhere in the luminous area around the central Mandelbrot fractal you can find copies of the Mandelbrot figure. If you zoom in on the figure there are an endless number of copies, which get smaller and smaller.
In a more mathematical depiction of the Mandelbrot fractal the self symmetry be come even more clear. With the enlargement of the picture new small spots appear. Which appear to be new Mandelbrot figures if you look closely. When this detail of the Mandelbrot fractal is colored it becomes visible that all fragment are connected via a complex network of curls and spirals to the biggest depiction of the fractal. So there is cohesion is the most perfect example of self symmetry!
Fractals seemed to have an important function in the description of things that appear as chaotic systems. It brings structure in messy looking systems like particles with an extreme rough surface, the leaf shape of plant or the branches structure of trees.
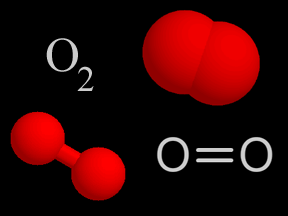
The perfect self symmetry is something but does there also exist something in nature like a perfect symmetry between two or more things. Researching this question I went into the building blocs of our world, the atoms. And even smaller. The atoms doesn’t appear in pairs necessary but in some molecules they does. An example of such a perfect symmetrical molecule is oxygen.
The oxygen molecule has both symmetry in the horizontal and vertical plane and has rotational symmetry as well. This quality of symmetry of the oxygen molecule provided by nature provides stability to the molecule. It will take a lot of energy to take break the bond between the two oxygen atoms.
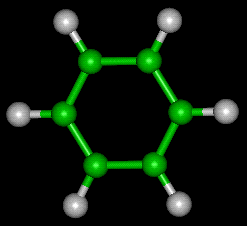
Symmetry is also present in some more complex molecules with more just two atoms. Benzene’s which consists out of 6 carbon atoms and 6 hydrogen atoms also has a high symmetry degree.
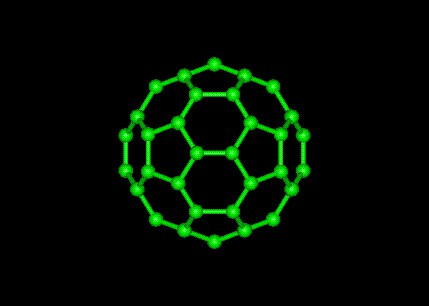
The benzene’s molecule has also as the oxygen molecule symmetry in the horizontal and vertical plane. But doesn’t has the rotational symmetry. But is has symmetry for a rotation of 180 degrees and inversion. An example of a real complex molecule is fullerene also called the bucky ball molecule because it has the structure of a bucky ball. It is constructed out of pentagons and hexagons.
As you can there are a lot of symmetrical elements present in this molecule. But the degree of symmetry has significant decreased compared to the oxygen molecule. So it tend to be in nature that structures when they grow bigger still have symmetry in their structure but not the perfect symmetry as I found in the simplest molecule consisting out of two atoms.
A pair of atoms can form a perfect symmetrical couple but if we zoom in deeper on natures building blocs we can find another really strange pair. The electron, a part of the atom, is always coupled to a partner electron. This couple is related to each other via something called spin. One of the electrons has spin up and the other has spin down. The exact location of this couple is strangely enough not to describe that is why it is described as a wave function. And it appears that those functions for the electron couples (orbitals) form perfectly symmetrical images.
With this research I was looking for symmetry starting from is visual esthetics. By zooming in on first the fractals I found that nature sometimes builds via the process of perfect self symmetry. And by looking into the smallest building blocs I found that also with this small elements nature has a preference for symmetry.